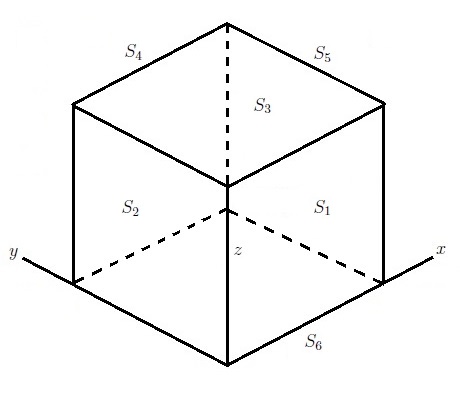
(b) \(S_i\) (\(i=1,2,\ldots ,6\))を, 左図の通りに定義する.

\(S_1\)についての積分は, 法線ベクトル\(n_1=(0,-1,0)\)より, \begin{align*} \iint _{S_1}A\cdot n_1dS_1&=\int_0^1 \int_0^1 \left( x^2y,xy,z\right) \cdot \left(0,-1,0\right) \Big|_{y=0}dxdz\\ &=\int_0^1 \int_0^1 0dxdz=0 \end{align*} \(S_2\)についての積分は, 法線ベクトル\(n_2=(-1,0,0)\)より, \begin{align*} \iint _{S_2}A\cdot n_2dS_2&=\int_0^1 \int_0^1 \left( x^2y,xy,z\right) \cdot \left(-1,0,0\right) \Big|_{x=0}dydz\\ &=\int_0^1 \int_0^1 0dxdz=0 \end{align*} \(S_3\)についての積分は, 法線ベクトル\(n_3=(0,0,1)\)より, \begin{align*} \iint _{S_3}A\cdot n_3dS_3&=\int_0^1 \int_0^1 \left( x^2y,xy,z\right) \cdot \left(0,0,1\right) \Big|_{z=1}dxdy\\ &=\int_0^1 \int_0^1 dxdy=1 \end{align*} 同様に, \(S_4,S_5,S_6\)についての積分を計算すると, \begin{align*} \iint _{S_4}A\cdot n_4dS_4&=\frac{1}{2}\\ \iint _{S_5}A\cdot n_5dS_5&=\frac{1}{2}\\ \iint _{S_6}A\cdot n_6dS_6&=0 \end{align*} よって, \begin{align*} \iint _S A\cdot ndS=\sum _{i=1}^6 \iint_{S_i}A\cdot n_idS_i=2 \end{align*}