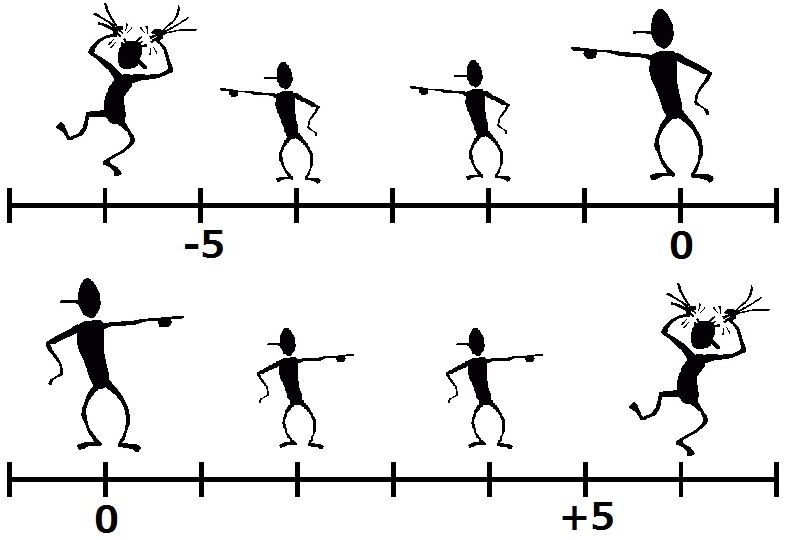
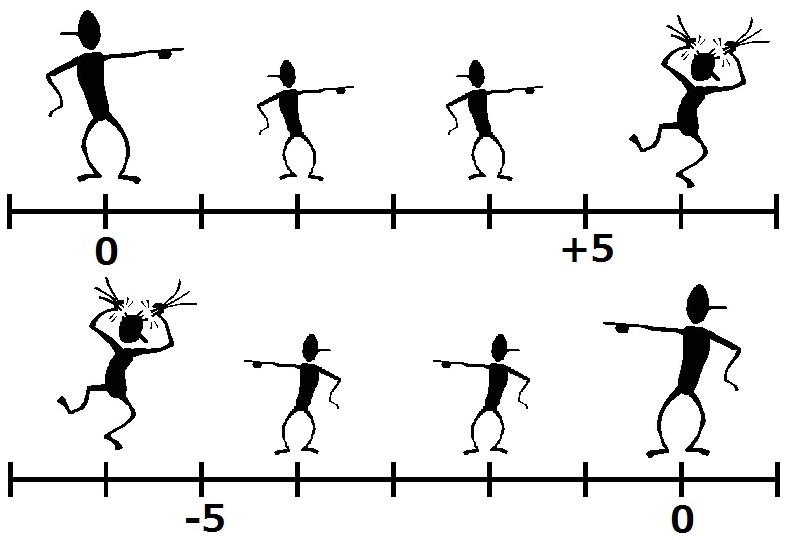
解説 (乗法・除法)
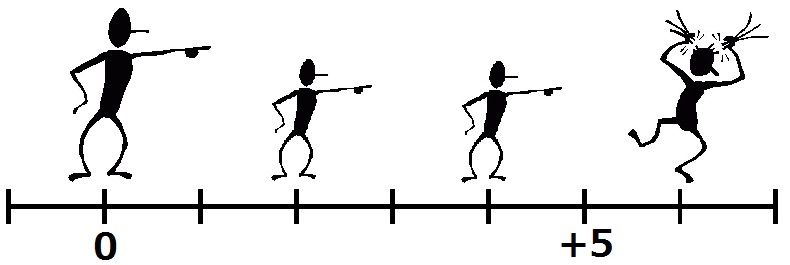
まず, 左の数直線を用いて, かけ算と割り算の意味について考えます.
\begin{equation}
2\times 3=6\label{mult1}
\end{equation}
\eqref{mult1}は, 2を足すことを, 3回繰り返すと, 6に到着すると解釈できます.
\begin{equation}
6\div 2=3\label{div1}
\end{equation}
一方, \eqref{div1}は, 6に到着するためには, 2を足すことが, 3回必要であると解釈できます.
つまり, かけ算は回数, 割り算は1回あたりの量を表します.