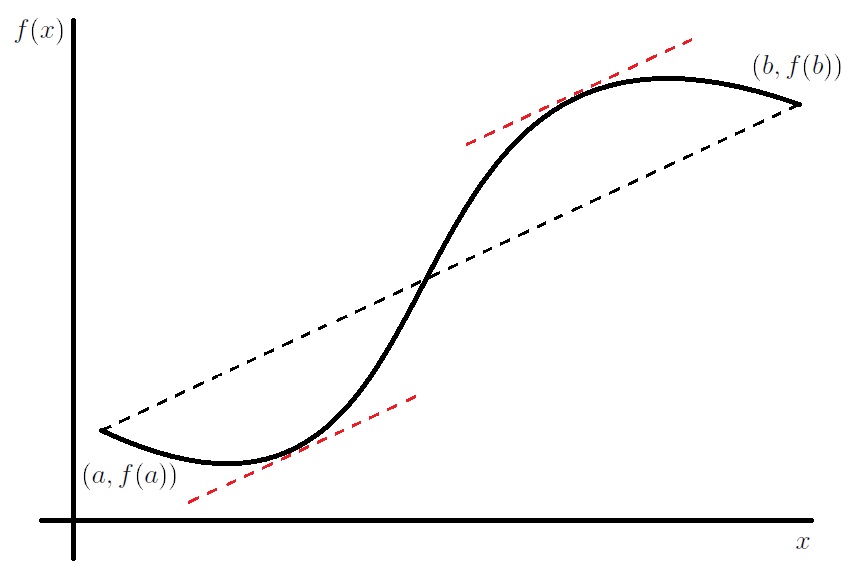
関数\(f(x)\)を, 左図の曲線とします. 端点\((a,f(a))\), \((b,f(b))\)を結ぶ線分の傾きは \begin{equation} \frac{f(b)-f(a)}{b-a}\label{grad} \end{equation} 左図から分かるように, \eqref{grad}と傾きが同じ点が2つあります. よって, 定理が成り立ちます.

ところで, 「開区間\((a,b)\)で微分可能」という条件は, 何のためにあるのでしょうか?
例として, 関数\(f(x)\)を, 第1象限における単位円とします. \begin{equation} f(x)=\sqrt{1-x^2}\quad (0 < x < 1)\label{circ} \end{equation} \eqref{circ}を微分すると \begin{equation} f'(x)=-\frac{x}{\sqrt{1-x^2}}\label{diff} \end{equation} \(x=1\)のとき, \eqref{diff}の分母は0になります. よって, 端点において, \(f(x)\)は微分できません. しかし, 右図から分かるように, 定理は成り立ちます.
このように, 端点で微分できない関数\(f(x)\)も考慮するために, 「開区間\((a,b)\)で微分可能」という条件があるのです.